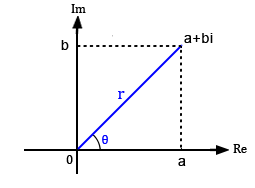
| Complex Numbers |
A Complex Number consists of a Real number and an Imaginary number. The calculator fully supports complex numbers, both in Rectangular and Polar forms.
Complex Number Forms:
 |
| Complex operators |
Imaginary Unit
Use this to enter the imaginary unit 'i' into a value or expression. The imaginary unit is calculated through multiplication, e.g., 5i is calculated as 5×i.
8 + 3 · = ➜ 8+3i
Polar Operator
Enter the Polar operator between two coordinates. The left value represents the distance (rho), and the right value represents the angle (θ - theta). The result is affected by the angle mode (degrees, radians, grads).
5 ∠ 1 8 0 = ➜ -5
Polar Display Format
To display the result in Polar form, perform a long press on the S⇌D button and select Polar Coordinates from the list. The POLAR indicator will be shown at the top of the screen.
TThe angular coordinate (θ - theta) is calculated according to the current angular unit mode of the calculator.
5i ➜ S⇌D (POLAR) ➜ 5 ∠ 90 DEG
| Complex Functions |
Argument
Argument - Calculates the argument (angle) of the complex value.
S ( 3 + 5 · ) = ➜ 1.0303768265
Conjugate
Conjugate - Calculates the conjugate of the complex value.
X ( 3 + 5 · ) = ➜ 3-5i
Real Part
Retrieves the real part of a complex value.
T ( 3 + 5 · ) = ➜ 3
Imaginary Part
Retrieves the imaginary part of a complex value.
U ( 3 + 5 · ) = ➜ 5